Sigma Notation

Sigma notation is used to write a very long sum (of elements) in a very concise manner. It is NOT used for writing any sum, rather it is the more convenient way of writing the sum of elements that follow a pattern. Sigma notation is referred to as a function as it does a job of adding terms.

Let us learn more about sigma notation along with how to write it using sigma symbol. Let us see the useful formulas that are related to summation.

What is Sigma Notation?

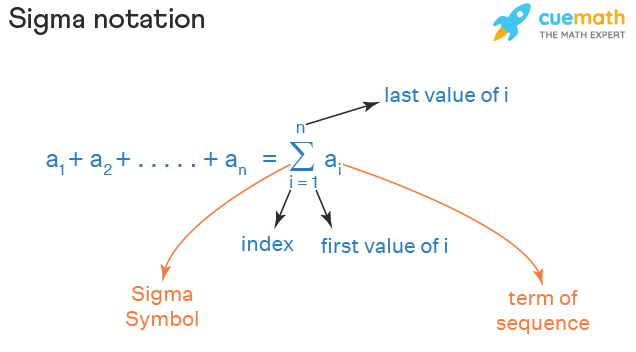
Sigma notation is the most easiest way of writing a very large sum of elements of a sequence in a simple manner. We know that a sequence is a collection of terms that follow a pattern and sigma notation is used to represent the sum of such elements. This is also known as summation notation as it represents a sum. The terms that are being added in sigma notation are called "summands" or "addends". For example, if we want to write the sum 2 + 4 + 6 + . + 50 (i.e., the sum of the first 25 even natural numbers) then we can write this sum easily using the sigma notation as \(\sum_^\) 2i. This is read as "sigma/summation of 2i where i goes from 1 to 25". Writing the sum using the summation notation was possible because the numbers 2, 4, 6, . 50 were following a pattern (or) they belong to the sequence \(_^\). In this notation,

• ∑ is the symbol that is pronounced as "sigma".
• "i" is called the index of summation
• 1 is the first value of n
• 25 is the last value of n.

When we expand the above sigma notation \(\sum_^\) 2i, we get 2(1) + 2(2) + . + 2(25) = 2 + 4 + . + 50 and we got the actual sum back. We can always cross check our sigma notation by expanding it. In general, the summation notation used to represent the sum of elements of a sequence i>\(_^\) looks as follows:

Sigma Symbol Math

As we have seen in the last section, the sigma symbol in math is ∑ which is pronounced as "sigma". This is one of the Greek alphabets. This sigma symbol is also known as "capital sigma". The summation notation written using the sigma symbol is also known as a "series" as it denotes a sum.

How to Write Sigma Notation?

From the above example, you might already have got an idea about how to write the sigma notation. Here are the steps in detail for writing the sum of terms as summation notation.

• Find the general term of the terms of the sum.
  If the sequence of terms is arithmetic / geometric then we can use the general term formula of the respective sequences. If not, we will find the general formula by investigation and observation.
• Select some alphabet (preferably a lowercase letter) to be the index. The usual letters we chose for the index of summation is "i" or "k".
• Observe the sequence and decide the first value and last value of the index.
• Finally, use the sigma symbol to write the sigma notation.

Note that the sigma notation is used to write a sum only when the terms of the sum follow a pattern. Any random sum, say 2 + 3 + 7 + 25 + 51, cannot be written using the sigma as we cannot find a general term in this case. Here is an example.

Example: Write the sigma notation for 16 + 25 + 36 + 49 + . + 100.

Solution:

It is clear that the sequence is neither arithmetic nor geometric. So we will just observe the terms. We can clearly see that the sequence can be written as squares, i.e., . If we take the index to be "i", then it is pretty clear that i goes from 4 to 10. Thus, the summation notation for the given sum is \(\sum_^\) i 2 .

How to Expand Summation Notation?

Expanding the summation notation is just the opposite process of writing it. Here are the steps for writing the same.

• Substitute every value of the index (starting from the first to last and increasing it by 1 every time) in the general term.
• Place a plus symbol between all such terms obtained from the last step.

Example: Let us consider the same sigma notation that we got in the last section \(\sum_^\) i 2 . Let us expand it by substituting the values of "i" to be 4, 5, 6, 7, 8, 9, and 10, one by one in the general term i 2 . Then we get 4 2 + 5 2 + 6 2 + 7 2 + 8 2 + 9 2 + 10 2 which is same as 16 + 25 + 36 + 49 + 64 + 81 + 100.

Expanding the sigma notation helps us to verify whether we have written the notation correctly.

Properties of Sigma Notation

• If there is a constant that is a multiple in the general term, then we can write it out of the notation. i.e., \(\sum_>^ k a_=k \sum_^ a_\), where 'k' is a constant.
• The summation notation can be split along the addition or subtraction. i.e.,
  \(\sum_>^\left(a_ \pm b_\right)=\sum_^ a_ \pm \sum_>^ b_\)
• The sigma notation cannot be split along the multiplication or division. i.e.,
  \(\sum_>^\left(a_ b_\right) \neq \sum_^ a_ \sum_>^ b_\)
  \(\sum_>^\dfrac< b_> \neq \dfrac<\sum_^ a_><\sum_>^ b_>\)
• \(\sum_>^ 1\) = 1 + 1 + 1 + . + 1 (n times) = n.
• \(\sum_>^ 0\) = 0 + 0 + . + 0 (n times) = 0.

Sigma Notation Formulas

Though all summations cannot be simplified using some formulas, there are some formulas derived to simplify some famous summation notations. These formulas are very helpful to find the sum of natural numbers, sum of squares of natural numbers, sum of cubes of natural numbers, sum of even numbers, sum of odd numbers, etc. Here is the list of sigma notation formulas:

☛ Related Topics:

• Summation Calculator
• Infinite Series Calculator
• Sum of Arithmetic Sequence Calculator
• Geometric Sequence Calculator

Sigma Notation Examples

Example 1: Write the following sum in sigma notation: 5 + 10 + 20 + 40 + . + 1280. Solution: The terms in the given sum are 5, 10, 20, 40, . 1280. Every term is obtained by multiplying its previous term by 2. So it is a geometric sequence with a common ratio r = 2 and first term a = 5. So its general term is: aₙ = ar n - 1 = 5(2) n - 1 . Now let 5(2) n - 1 = 1280
Dividing both sides by 5,
(2) n - 1 = 256
2 n - 1 = 2 8
n - 1 = 8
n = 9 So the given sum can be written as the sigma notation: \(\sum_>^\) 5(2) n - 1 . Answer: The given sum using summation notation is \(\sum_>^\) 5(2) n - 1 .

Example 2: Expand the summation notation \(\sum_>^ <\infty>\dfrac\) as a series. Solution: The index of the given summation is from 1 to ∞. So we will substitute the numbers 1, 2, 3, . upto infinity in the general term \(\dfrac\) and put a plus sign between every two terms. Then we get: \(\dfrac+\dfrac +\dfrac + . \) = \(\dfrac + \dfrac+ \dfrac+. \) Answer: The given series is expanded as \(\dfrac + \dfrac+ \dfrac+. \).

Become a problem-solving champ using logic, not rules. Learn the why behind math with our certified experts